Understanding Support Vector Machines (SVM): A Comprehensive Guide

 

Introduction

Support Vector Machines (SVM) are powerful and versatile machine learning algorithms used for both classification and regression tasks. Developed in the 1960s and further refined in the 1990s, SVMs have proven to be a reliable and efficient tool for various applications, such as image classification, text categorization, and anomaly detection. In this blog post, we'll take an in-depth look at SVMs, exploring their principles, mathematical foundations, applications, and key considerations for implementation.

What is an SVM?

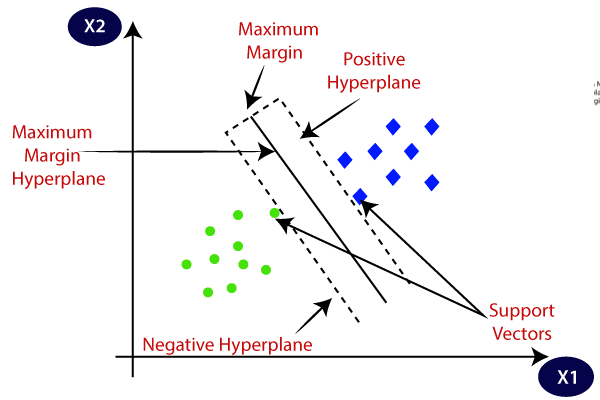
At its core, an SVM is a supervised machine learning algorithm that seeks to find the best possible decision boundary or hyperplane that separates data points belonging to different classes. It does this by maximizing the margin between the nearest data points of each class, which are known as support vectors. These support vectors play a critical role in defining the hyperplane and make SVMs particularly robust and resistant to overfitting.

 

How SVM Works

1. Linear Separation

In the simplest form, SVMs aim to find a hyperplane that linearly separates two classes of data points. The equation of a hyperplane in a two-dimensional space (for binary classification) can be represented as:

$\vec{w}\cdot \vec{x}+b=0$

$\cdot x$

$+b=0$

Here, $\vec{w}$

is the weight vector perpendicular to the hyperplane, $\vec{x}$ is the input data vector, and $b$ is the bias term. SVMs find the optimal $\vec{w}$

and $b$ values that maximize the margin between the two classes while ensuring correct classification.

2. Margin Maximization

The margin is the distance between the hyperplane and the nearest data point from either class. SVMs aim to maximize this margin, as a larger margin often leads to better generalization and improved performance on unseen data. Mathematically, the margin is given by:

$\text{margin}=\frac{2}{\mathrm{\parallel }\vec{w}\mathrm{\parallel }}$

$\frac{\Vert }{2}$

3. Dealing with Non-Linearity

In cases where the data is not linearly separable, SVMs can still be used effectively. They employ kernel functions like polynomial and radial basis function (RBF) kernels to map the data into a higher-dimensional space where linear separation is possible. This allows SVMs to handle complex decision boundaries.

SVM Applications

SVMs find applications in a wide range of domains, including:

1. Image Classification: SVMs are commonly used in computer vision tasks like object recognition and face detection.

2. Text Classification: Spam email detection and sentiment analysis are examples of text classification tasks where SVMs have been successful.

3. Bioinformatics: SVMs are employed in DNA sequence classification, protein structure prediction, and disease diagnosis.

4. Finance: SVMs can be used for credit scoring, stock market prediction, and fraud detection.

5. Handwriting Recognition: SVMs have been applied to handwritten digit recognition in digitizing postal addresses and bank checks.

Key Considerations for SVM Implementation

When working with SVMs, here are some essential considerations:

1. Kernel Selection: Choosing the right kernel function is crucial. Linear kernels are suitable for linearly separable data, while non-linear kernels like RBF are better for complex datasets.

2. Regularization Parameter (C): The parameter C controls the trade-off between maximizing the margin and minimizing classification errors. A smaller C value leads to a larger margin but may allow some misclassification, while a larger C value reduces the margin but aims for stricter classification.

3. Data Preprocessing: SVMs are sensitive to the scale of features, so it's essential to scale or normalize your data before training.

4. Handling Imbalanced Data: If your dataset has imbalanced class distributions, consider techniques like oversampling, undersampling, or using class weights to mitigate the issue.

5. Cross-Validation: Always use cross-validation to assess the SVM's performance and tune hyperparameters effectively.

6. Model Interpretability: SVMs offer relatively low model interpretability compared to other algorithms like decision trees or logistic regression. Consider this when choosing the right algorithm for your problem.

Conclusion

Support Vector Machines (SVMs) are a powerful and versatile tool in the machine learning arsenal. Their ability to handle both linear and non-linear classification tasks, along with their robustness and effectiveness, makes them a popular choice in various fields. However, understanding the mathematics behind SVMs and fine-tuning hyperparameters are crucial for achieving optimal results. With the right approach and careful consideration of your problem, SVMs can be a valuable asset in your machine learning toolbox.

Reference